Image Segmentation by Region Growing and Spectral Clustering with a Natural Convergence Criterion NOTE: This paper was published in the Proceedings of the 1998 International Geoscience and Remote Sensing Symposium (IGARSS '98), Seattle, WA, July 6-10, 1998.

Image Segmentation by Region Growing and Spectral Clustering with a Natural Convergence Criterion

James C. Tilton NASA's Goddard Space Flight Center Mail Code 935, Greenbelt, Maryland 20771 USA Telephone: (301) 286-9510 / Facsimile: (301) 286-1776 Email: James.C.Tilton@gsfc.nasa.gov

Abstract -- The image segmentation approach described herein is a new hybrid of region growing and spectral clustering. This approach produces a specified number of hierarchical segmentations at different levels of detail, based upon jumps in a dissimilarity criterion. A recursive implementation of this segmentation approach on a cluster of 66 Pentium Pro PCs is described, and the effectiveness of this segmentation approach on Landsat Multispectral Scanner data is discussed.

INTRODUCTION

The image segmentation approach described herein was developed from earlier work described in [1], and is related to image segmentation approaches developed in [2-3]. The current version contains several refinements. One key refinement is an alternation between region growing and spectral clustering. However, the region growing process still controls the segmentation process, since the region growing process sets the threshold for spectral clustering, and spectral clustering is restricted from merging spatially adjacent regions. Another key refinement is the development of a method to produce a prespecified number of significant hierarchical segmentation results. These results are derived from a set of raw segmentations identified as the segmentations occurring the iteration before significant jumps in the ratio of the dissimilarity criterion from one iteration to the next. The final set of hierarchical segmentations is selected by starting from the last (most coarse) segmentation so identified and recursively splitting the region with the highest global dissimilarity value by backtracking to the next earlier raw segmentation in which that region is split.

After a more detailed description of the segmentation approach, an implementation on a cluster of 66 Pentium Pro PCs is described, and the effectiveness of this segmentation approach on Landsat Multispectral Scanner (MSS) data is discussed.

HYBRID OF REGION GROWING AND SPECTRAL CLUSTERING

A high-level outline of the new hybrid image segmentation approach is as follows:

Label each image pixel as a separate region and set the global criterion value, critval, equal to zero.
Calculate the dissimilarity criterion value between each spatially adjacent region.
Find the smallest dissimilarity criterion value, and merge all pairs of spatially adjacent regions with this criterion value.
Calculate the dissimilarity criterion value between all pairs of non-spatially adjacent regions.
Merge all pairs of non-spatially adjacent regions with dissimilarity criterion value less than or equal to the criterion value found in step 3.
If the number of regions remaining is less than the preset value minregions, go to step 7. Otherwise go to step 2.
Let prevcritval = critval. Reset critval to be the current global criterion value. If prevcritval = zero, go to step 2. Otherwise calculate cvratio = critval/prevcritval. If cvratio is greater than the preset threshold convfact, save the region label map from the previous iteration as a "raw" segmentation result. If the number of regions remaining is two or less, save the region label map from the current iteration as the coarsest instance of the final hierarchical segmentation result, and go to step 8. Otherwise go to step 2.
Calculate the global criterion value over each region separately. For the region with maximum global criterion value, search backwards from the last "raw" segmentation result (from step 7) to an iteration where this region is split into two or more regions. Replace the labeling for this region with the labeling from the found iteration and store as the next more detailed level of the final hierarchical segmentation. Repeat this step until the preset number of levels in the final hierarchical segmentation is obtained.

Dissimilarity Criterion

Selection of an appropriate dissimilarity criterion is generally dependant on the application the resulting segmentations will be used for, and on the characteristics of the image data. Nevertheless, we have developed and studied a few general purpose similarity criteria for use with this algorithm, including criteria based on minimizing mean-square error and minimizing change in image entropy [4], and the "Normalized Vector Distance" from [5]. The "Euclidean Spectral Distance" (from [3]) is used as the dissimilarity criterion in the tests described later in this paper.

For two regions i and j, characterized by the mean vectors X_i = (x_1i, x_2i,..., x_ci)^T and X_j = (x_1j, x_2j,..., x_cj)^T, the Euclidean Spectral Distance (ESD) is defined as:

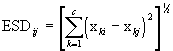(1)

where c is the number of spectral channels.

Global Criterion

The global criterion is used to identify significant changes in the segmentation results from one iteration to the next. This criterion is same as the dissimilarity criterion, except that it compares the original image data with the region mean image from the current segmentation. The value of this criterion is calculated at each image point and averaged over the entire image.

The global criterion is also used to select which region is to be split in the final, backtracking stage of the algorithm. In this case the value of this criterion is calculated at each image point in the region under consideration, and is averaged over that region.

Parameter Settings

For the Landsat MSS data sets we have tested, we have found reasonable values for minregions to be in the range of 512 to 1024, or about one-half the total number of pixels in the image, whichever is less. Smaller values for minregions can produce image artifacts due to the divide-and-conquer, recursive implementation method (which is described later in this paper). Larger values result in longer execution times. For the same data sets, we have also found reasonable values for convfact to be in the range of 1.001 to 1.010.

Discussion

Steps 2 and 3 make up the region growing portion of the algorithm and steps 4 and 5 constitute the spectral clustering portion. These region growing and spectral clustering steps are iterated until two or fewer regions remain. Results from these iterations are selectively saved in step 7 for the backtracking stage (step 8) based on the values of minregions and convfact. This set of "raw" segmentations saved in step 7 are analyzed in step 8 to produce the final set of hierarchical segmentations. In order to make viewing of the results more convenient, the region labels can be renumbered from largest region to the smallest. The convention employed is to label the "no data" areas as "0," and the largest region as "1."

IMPLEMENTATION ON THE HIVE

This hybrid image segmentation algorithm is very computationally intensive. In particular, step 4 requires the calculation of the dissimilarity criterion value between each region and every other region in the image. A divide-and-conquer, recursive approach for implementing this algorithm has been devised to reduce the computational load. Further, the nature of this divide-and-conquer, recursive approach is such that it can be implemented very effectively on a set of tightly networked, distributed computers configured as a Beowulf-class parallel computer [6]. In particular, this algorithm has been implemented on a Beowulf-class parallel computer call "the HIVE" that consists of 66 Pentium Pro PCs (64 slaves and 2 controllers) with two processors per PC.

The divide-and-and conquer, recursive implementation of the hybrid image segmentation algorithm is as follows:

Specify the number of levels of recursion required (nblevels), and pad the input image, if necessary, so that the width and height of the image can be evenly divided by nblevels. Set level = nblevels. (A good value for nblevels results in the image section at level=1 consisting of roughly 500 to 2000 pixels.)
Call recur_seg(level,image).

Outline of recur_seg(level,image):

If level > 1, divide the image data into quarters (in half in the width and height dimensions) and call recur_seg(level-1,image/4) for each image quarter (represented as image/4). Otherwise go to step 3.
After all four calls to recur_seg() from step 1 complete processing, reassemble the image segmentation results.
Execute the image segmentation algorithm outlined in the section HYBRID OF REGION GROWING AND SPECTRAL CLUSTERING with the following modification: If level < nblevels, terminate the algorithm when the number of regions reaches minregions/2, and do not check for critval or output any "raw" segmentation results.

Separate instances of the program recur_seg() are spawned for each call to recur_seg().

SEGMENTATION RESULTS

Prior to the implementation of this algorithm on the HIVE, the largest image that was segmented with this hybrid image segmentation algorithm was a 1024x 1024-pixel, 4-band Landsat MSS image. This image was processed on a MasPar MP-2 massively parallel computer (with 16,384 processors) using a simulation of the divide-and-conquer approach with three levels of recursion. If 16 MasPar MP-2 computers were used, the processing would have completed in about 3.4 hours. The HIVE implementation takes less than 0.4 hours to segment the same image. (NOTE: A revised implementation on the MasPar, incorporating lessons learned from the HIVE implementation, is expected to reduce the MasPar processing time.)

The recursive version of the hybrid image segmentation has also been implemented on a conventional UNIX workstation. Table 1 compares wall clock run-times for segmentation using the HIVE as compared to a conventional workstation.

To demonstrate the effectiveness of the hybrid image segmentation algorithm in selecting out important region features from image data, it would be best to show several color pictures illustrating segmentations at several levels of detail. However, this is not possible in the restricted format of this proceedings. Such pictures will be provided during the oral presentation of this paper.

As a poor substitute for several color pictures, a verbal description of some segmentation results from a Landsat MSS scene (same as in Table 1) is given here. The coarsest segmentation is just two regions: one consists of nearly the whole image, while the other consists of two pixels of data that appears to be from a data anomaly. The next finer segmentation consists of seven regions, including some clouds, lakes and rivers, and some bright agricultural fields. At the finer segmentation levels, even more difficult features such as small roads and different lake depths are distinguished.

REFERENCES

[1] J. C. Tilton, "Image segmentation by iterative parallel region growing and splitting," Proc. 1989 International Geoscience and Remote Sensing Symposium, pp. 2235-2238, Vancouver, Canada, 1989.

[2] J.-M. Beaulieu and M. Goldberg, "Hierarchy in Picture Segmentation: A Stepwise Optimization Approach," IEEE Transactions on Pattern Analysis and Machine Intelligence, 11 (2), pp. 150-163, 1989.

[3] R. P. H. M. Schoenmakers, Integrated Methodology for Segmentation of Large Optical Satellite Image in Land Applications of Remote Sensing, Agriculture series, Catalogue number: CL-NA-16292-EN-C, Luxembourg: Office for Official Publications of the European Communities, 1995.

[4] J. C. Tilton, "Experiences using TAE-Plus command language for am image segmentation program interface," Proceedings of the TAE Ninth Users' Conference, New Carrollton, MD, pp. 297-312, 1991.

[5] A. Baraldi and F. Parmiggiani, "A neural network for unsupervised categorization of multivalued input patterns: an application to satellite image clustering," IEEE Transactions on Geoscience and Remote Sensing, vol. 33, no. 2, 305-316, 1995.

[6] D. J. Becker, T. Sterling, D. Savarese, J. E. Dorband, U. A. Ranawake, C. V. Parker, "Beowulf: A parallel workstation for scientific computation," Proceedings of the International Conference on Parallel Processing, 1995.

Table 1. Wall clock run times in minutes for the recursive implementation of the hybrid image segmentation algorithm on the HIVE and on a 167-MHz SunULTRA Model 170E Workstation. The image processed is a 4-band Landsat MSS scene of north central Canada obtained on Aug. 12, 1984. For this test minregions = 512 and convfact = 1.005. The refinement stage (step 8) is not included in these timings.

Image Size	the HIVE	Sun ULTRA
3456x2688	134.9 minutes	NA
1728x1344	34.3 minutes	NA
864x672	11.5 minutes	NA
432x336	5.6 minutes	127.7 minutes
216x168	3.7 minutes	52.8 minutes
108x84	2.3 minutes	13.0 minutes
54x42	1.4 minutes	1.8 minutes