A Recursive PVM Implementation of an Image Segmentation Algorithm with Performance Results Comparing the HIVE and the Cray T3E
Abstract
1: Introduction
Image segmentation is a partitioning of an image into sections or regions. These regions may be later associated with ground cover type or land use, but the segmentation process simply gives generic labels (region 1, region 2, etc.) to each region. The regions consist of groupings of multispectral or hyperspectral image pixels that have similar data feature values. These data feature values may be the multispectral or hyperspectral data values themselves and/or they may be derived features such as band ratios [1] or textural features [2].Image segmentation is a key first step in a number of approaches to image analysis and image compression. In image analysis, the group of pixels contained in each region provides a good statistical sampling of data values for more reliable labeling based on multispectral or hyperspectral feature values. In addition, the region shape can be analyzed as an additional clue for the appropriate labeling of the region. In image compression, the regions form a basis for compact representation of the image data [3].
Most image segmentation approaches can be placed in one of three classes [4]:
- characteristic feature thresholding or clustering,
- boundary detection, or
- region growing.
With region growing, spectrally similar but spatially disjoint regions are never associated together, and it is often not clear at what point the region growing process should be terminated. Also, region growing tends to be a computationally intensive process.
We have developed a hybrid region growing and spectral clustering approach (first described in [5]) that largely overcomes these problems. The hybridization with spectral clustering allows association of spectrally similar but spatially disjoint regions. The approach also includes the detection of natural convergence points to assist in determining at what point the region growing process should terminate. Finally, the recursive version of this approach is very effectively implemented on MIMD (Multiple Instruction, Multiple Data stream) parallel computers, which greatly reduces the amount of time required to segment large images with this approach. The main subject of this paper is the description and discussion of this implementation on two MIMD parallel computers: the HIVE and the Cray T3E.
After a description of the segmentation approach, the recursive version of the algorithm is described, and the minor implementation differences between the HIVE and Cray T3E are pointed out. Then timing results are presented for a SunULTRA workstation, the HIVE and the Cray T3E.
2: Hybrid of Region Growing and Spectral Clustering
A high-level outline of the hybrid image segmentation (HSEG) approach is as follows:- Label each image pixel as a separate region and set the global criterion value, critval, equal to zero.
- Calculate the dissimilarity criterion value between each spatially adjacent region.
- Find the smallest dissimilarity criterion value, and merge all pairs of spatially adjacent regions with this criterion value.
- Calculate the dissimilarity criterion value between all pairs of non-spatially adjacent regions.
- Merge all pairs of non-spatially adjacent regions with dissimilarity criterion value less than or equal to the criterion value found in step 3.
- If the number of regions remaining is less than the preset value minregions, go to step 7. Otherwise go to step 2.
- Let prevcritval = critval. Reset critval to be the current global criterion value. If prevcritval = zero, go to step 2. Otherwise calculate cvratio = critval/prevcritval. If cvratio is greater than the preset threshold convfact, save the region label map from the previous iteration as a "raw" segmentation result. If the number of regions remaining is two or less, save the region label map from the current iteration as the coarsest instance of the final hierarchical segmentation result, and stop. Otherwise go to step 2.
2.1: Dissimilarity Criterion
Selection of an appropriate dissimilarity criterion is generally dependent on the application the resulting segmentations will be used for, and on the characteristics of the image data. Nevertheless, we have developed and studied a few general purpose similarity criteria for use with this algorithm, including criteria based on minimizing mean-square error and minimizing change in image entropy [6], and the "Normalized Vector Distance" from [7]. The "Euclidean Spectral Distance" (from [8]) is used as the dissimilarity criterion in the tests described later in this paper.For two regions i and j, characterized by the mean vectors Xi= (x1i, x2i, ..., xci)Tand Xj = (x1j, x2j, ..., xcj)T, the Euclidean Spectral Distance (ESD) is defined as:
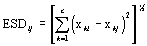 (1)
(1)where c is the number of spectral channels. We have found the ESD to be a good general purpose criterion.
2.2: Global Criterion
The global criterion is used to identify significant changes in the segmentation results from one iteration to the next. This criterion is same as the dissimilarity criterion, except that it compares the original image data with the region mean image from the current segmentation. The value of this criterion is calculated at each image point and averaged over the entire image.2.3: Parameter Settings
For the Landsat MSS data sets we have tested, we have found reasonable values for minregions to be in the range of 512 to 1024, or about one-half the total number of pixels in the image, whichever is less. Smaller values for minregions can produce image artifacts due to the divide-and-conquer, recursive implementation method (which is described later in this paper). Larger values result in longer execution times. For the same data sets, we have also found reasonable values for convfact to be in the range of 1.001 to 1.050.2.4: Discussion
Steps 2 and 3 make up the region growing portion of the HSEG algorithm and steps 4 and 5 constitute the spectral clustering portion. These region growing and spectral clustering steps are iterated until two or fewer regions remain. Results from these iterations are selectively saved in step 7 for later analysis based on the values of minregions and convfact. In order to make viewing of the results more convenient, the region labels can be renumbered from largest region to the smallest. The convention employed is to label the "no data" areas as "0," and the largest region as "1."3: Recursive, Divide-and-Conquer Implementation
The HSEG algorithm is very computationally intensive. In particular, step 4 requires the calculation of the dissimilarity criterion value between each region and every other region in the image. A divide-and-conquer, recursive approach for implementing this algorithm has been devised that is particularly amenable to implementation on MIMD parallel computers.The divide-and-conquer, recursive implementation of the HSEG algorithm is as follows:
- Specify the number of levels of recursion required (nblevels), and pad the input image, if necessary, so that the width and height of the image can be evenly divided by nblevels. Set level = nblevels. (A good value for nblevels results in an image section at level=1 consisting of roughly 500 to 2000 pixels.)
- Call recur_hseg(level,image).
- If level > 1, divide the image data into quarters (in half in the width and height dimensions) and call recur_hseg(level-1,image/4) for each image quarter (represented as image/4). Otherwise go to step 3.
- After all four calls to recur_hseg() from step 1 complete processing, reassemble the image segmentation results.
- Execute the HSEG algorithm as described in Section 2 above with the following modification: If level < nblevels, terminate the algorithm when the number of regions reaches minregions/fact, and do not check for critval or output any "raw" segmentation results (if level < nblevels-1, fact = 2; otherwise fact = 1).
4: Implementation on MIMD Parallel Computers
The recursive HSEG (RHSEG) algorithm has been implemented in the programming language "C" with calls to PVM routines [9] on both the HIVE and the Cray T3E parallel computers. The HIVE is a Beowulf-class parallel computer consisting of 66 Pentium Pro PCs (64 slaves and 2 controllers) with 2 200 Mhz processors per PC (for 128 total slave processors) which was developed and assembled by the Applied Information Sciences Branch at NASA's Goddard Space Flight Center [10]. The Cray T3E supercomputer is a model T3E-600 with 300 Mhz DEC EV5 processors with 4-way superscalar yielding a peak speed of 600 MF/PE. This supercomputer is installed at the NASA Center for Computational Science (NCCS) at NASA's Goddard Space Flight Center. While the Cray T3E has 1024 Pes, in the NCCS configuration only 512 Pes are available at a time to a given user. Both of these parallel computers are of the MIMD type.
The only difference between the HIVE and Cray T3E implementations of the algorithm is in the very first part of the program. In the HIVE implementation, individual tasks are spawned, with the PVM routine pvm_spawn(), while in the Cray T3E implementation, the required number of PEs (equal to the number of tasks) are allocated, with the special Cray PVM routine start_pes(). In the HIVE implementation, the tasks are spawned, parameters are broadcast, and the recursion is initiated from the special "drone" processor. On the Cray T3E there is no equivalent to the special "drone" processor (all PEs are equivalent), so the last PE allocated serves the role of the HIVE's "drone" on the Cray T3E. The "master" routine is run on the HIVE's "drone" processor, or on the corresponding PE on the Cray T3E (the last PE allocated). The "slave" routine is run on all other processors. The only other difference between the HIVE and Cray T3E implementations is in the declaration of some of the data arrays due to the different bit length of integers and short integers on the two machines.
4.1: Task or PE Allocation
The most obvious and straightforward approach to controlling the allocation of processing to tasks or PEs is to have each recursive call go to a different task or PE. However, with this approach it takes only five levels of recursion before the available 512 PEs on the Cray T3E are exceeded (1366 PEs would be required). While it would be possible to request the required 1366 tasks (1365 "slave" tasks plus the one "master" task on the drone) on the HIVE, this would require that each PE on the HIVE run 10 or 11 tasks, which is undesirable.
An approach that requires substantially fewer tasks or PEs is as follows: Instead of running the four calls to recur_hseg() to four separate tasks or PEs at each level of recursion, make just two of the calls and wait for these calls to return before making the remaining two calls, reusing the two tasks or PEs employed for the first two calls. This approach requires only 64 PEs or tasks at five levels of recursion compared to the 1366 tasks with the approach in which all four calls are made immediately to separate PEs or tasks.
A problem with the second approach is that it takes eight levels of recursion before all 512 available PEs are utilized on the Cray T3E, or the equivalent 512 tasks are required on the HIVE. The available parallelism is not utilized for images of sizes that require fewer levels of recursion. The solution to this underutilization is use a hybrid of the two approaches, in which four immediate calls to recur_hseg() are made at the higher levels of recursion and two immediate calls and two delayed calls (reusing PEs or tasks from the first two calls) are made at the lower levels of recursion. In this way the maximum possible parallelism is exploited without requiring an excessive number of PEs or tasks.
The number of PEs or tasks required, which recursive levels make 4 immediate calls, and which recursive levels make 2 immediate calls and 2 delayed calls is listed in Table 1 for several different levels of recursion. Also included is the image size that could be processed for each of the levels of recursion assuming the image size at the base level is 32 by 32 pixels. With a base level image size of 32 by 32 pixels, the largest image that can be processed limiting to 512 PEs or tasks is 8192 by 8192 pixels. Larger images can be processed by performing the higher levels of recursion on another workstation (equipped with a generous amount of RAM).
We are currently limited on the Cray T3E to processing images of size on the order of 4096 by 4096 pixels due to RAM constraints on the Cray T3E. The Cray T3E has 116 MB RAM per PE, while the HIVE is equipped with 293 MB (including 64 MB virtual) RAM per PE. RAM requirements are also increased on the Cray T3E because short integer arrays are 32 bits on the Cray T3E, while they are only 16 bits on the HIVE.
4.2: Task Flow and Communication Between Tasks
Upon initiation of the "master" program, the input data is copied to the appropriate processor's local disk on the HIVE, or to the system defined temporary directory on the Cray T3E (all Pes have direct access to this temporary directory on the Cray T3E).
After all tasks have been spawned or allocated, general parameters such as nbands (number of spectral bands) and minregions are broadcast from the "master" routine to all the "slave" routines. The recursive processing is initiated with the "master" routine through the passing of recursion level specific parameters to the first "slave" routine. Each "slave" routine at level > 1 passes on recursion level specific parameters in turn to its subsidiary "slave" routines. The level = 1 "slave" routines read the input data and perform hybrid region growing and spectral clustering. When the subsidiary "slave" routines at level < nblevels complete execution of HSEG, they send the resulting region label map data and region feature data back to the "slave" routine that called it.
When the calling "slave" routines at level > 1 receive the region label map and region feature data from their subsidiary "slave" routines, these calling "slave" routines assemble the region label map and region feature data for their level of recursion. After all subsidiary "slave" routines (four per calling routine) return their results, the calling "slave" routine starts execution of HSEG on the assembled region label map and region feature data. This process continues at all levels of recursion until the "slave" routine operating at level = nblevels receives the region label map and region feature data from the four subsidiary "slave" routines it called. After this last "slave" routine completes execution of HSEG on its assembled data, it reports its results back to the "master" routine, which formats and reports the results back to the user.
Minimal interprocessor communication is required with this implementation of RHSEG. Interprocessor communication is needed only at task initiation and completion. No interprocessor communication is utilized while each "slave" routine is actually performing the HSEG algorithm.
With this task flow, maximum MIMD parallelism is utilized when all "slave" routines are operating at level = 1 recursion. For the case of a 8192x8192 pixel image using 9 levels of recursion (see Table 1) with 512 total available tasks or Pes, 256 tasks or Pes are active at level = 1 recursion. When all level = 2 "slave" routines are active, only 128 tasks or Pes are active. Finally at level = nblevels (9 in this case), only one PE is active.
If we assume that the HSEG algorithm takes the same amount of time at each level of recursion, we can calculate the percentage utilization of the available parallelism for this implementation. This assumption is good if each task at each level of recursion starts and end with the same number of regions, which is usually the case for the middle levels of recursion. At the top level of recursion this implementation stops at twice the number of regions as the other levels. At the lowest level of recursion, the number of regions at the start of hybrid region growing and spectral clustering depends on the number of pixels in the smallest division of the image data. This being the case, this estimate of percentage utilization is only approximate. For the case of a 8192x8192 pixel image using 9 levels of recursion and with full task reuse, the average MIMD utilization of 512 processors is:
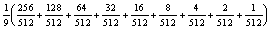
or about 11%. Despite this relatively low level average utilization of the available parallelism, this implementation is still very effective at providing practical processing times for image sizes of interest, as documented in the final section.
The HIVE has only 128 processors, but 512 tasks can be spread across the 128 processors (4 tasks each). Assuming that a processor with 2 active tasks runs at half speed, the average MIMD utilization of 128 processors with 512 tasks is:
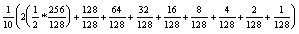
or about 40%.
We should point out that the average MIMD utilization is somewhat higher for smaller images were task reuse is not utilized. The largest image size where task reuse is not required with 512 available Pes is a 512x512 pixel image (Table 1). For this sized image, using the required 342 Pes on the Cray T3E, the average MIMD utilization is:
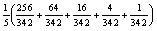
or about 20%, versus 11% with full task reuse. The average MIMD utilization on the HIVE (with 128 processors) is:
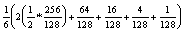
or about 44%, versus 40% with full task reuse.
4.3: Further Implementation Details
The HSEG algorithm requires the calculation of a dissimilarity criterion value between spatially adjacent, and between spatially non-adjacent regions. An efficient implementation approach is to store the region feature information in "C" structures that are linked together in a pair of ordered linked lists. The "C" structure used to store region feature information is defined as follows:
{
unsigned short label;
unsigned short npix;
double *mean;
struct R_LIST *nghbr;
struct REGION *bnghbr;
float bncomp;
struct REGION *bregion;
float brcomp;
struct REGION *mgreg;
double critval;
} reg_struct;
In the "REGION" structure defined above, "label" is the numeric region label, "npix" is the number of pixels in the region, "*mean" defines a storage location for the region mean vector, "*nghbr" defines a storage location for a list of neighbor regions, "*bnghbr" is a pointer to the REGION structure of the most similar neighboring region, "bncomp" is the dissimilarity criterion value with the most similar neighboring region, "*bregion" is a pointer to the REGION structure of the most similar non-adjacent region, "brcomp" is the dissimilarity criterion value with the most similar non-adjacent region, "*mgreg" is a pointer to the REGION structure this region has been merged into (this is NULL if this region has not been merged into another region), and "critval" is the partial sum of the global criterion value for this region ("critval" is only utilized in the last stage).
The "C" structure for the ordered linked lists is as follows:
{
struct REGION *link;
struct R_LIST *next;
unsigned char active_flag;
} reg_list;
where "*link" is a pointer to the REGION structure containing the information for the referred to region, "*next" is a pointer to the next element in the linked list, and "active_flag" is TRUE when this particular link is valid.
The spatial structure of the region labels must be maintained throughout the region growing process. This is accomplished with the following "C" structure:
{
struct REGION *link;
} reg_lblmap;
where "*link" is a pointer to the REGION structure containing the information for the referred to region. The array storing the spatial structure of region label map is an array of "C" structures of type R_LMAP of the same spatial size as the input image data.
Using ordered linked lists employing the REGION and R_LIST structures above, the only time exhaustive intercomparison of regions is required is during the initialization of the structure. A full sort of the ordered lists (one in order of minimum to maximum "bncomp" and one in order of minimum to maximum "brcomp") is also only required during structure initialization.
When a pair of regions are merged, the REGION structure with the lowest value "label" is updated with the new feature information. The only variable updated in the other REGION structure is "*mgreg," which is set to point to the REGION structure of the region this region is being merged into. The two neighbor lists, "*nghbr," are merged, and the dissimilarity criterion values are calculated between this region and the regions in the merged neighbor list. Then "*bnghbr" and "bncomp" are updated for the merged region and the neighboring regions. Next, the dissimilarity criterion values are calculated between this region and all non-adjacent regions, and the values of "*bregion" and "brcomp" are updated as needed. If the number of regions is less than minregions, the partial sum of the global criterion value is updated for the newly merged region. Finally, the ordered lists are updated by deleting the "merged out" region from the lists and resorting the lists to place the newly merged region into its proper position in the lists.
5: Segmentation Timing Results
Prior to the implementation of this algorithm on the HIVE and the Cray T3E, the largest image that was segmented with this hybrid image segmentation algorithm was a 1024´1024-pixel, 4-band Landsat MSS image. This image was processed on a MasPar MP-2 massively parallel computer (with 16,384 processors) using a simulation of the divide-and-conquer approach with three levels of recursion. If 16 MasPar MP-2 computers were used, the processing would have completed in about 3.4 hours. The HIVE implementation takes less than 0.4 hours to segment the same image. (NOTE: A revised implementation on the MasPar, incorporating lessons learned from the HIVE implementation, would be expected to reduce the MasPar processing time.)
The recursive version of the hybrid image segmentation has also been implemented on a conventional UNIX workstation. Table 2 compares wall clock run-times for segmentation using the HIVE as compared to a conventional workstation. These wall clock run times are end-to-end typically encountered on a quiet, but not stand-alone, system, and include data I/O and reformatting. Even on the runs on the HIVE, the final stage of processing occurs on the SunULTRA workstation. Even so, the timing ratio of 97 obtained on the largest image size is impressively close to the number of processors available on the HIVE (128). Concerning price vs. performance, the SunULTRA workstation utilized here cost $21K in 1996, and the HIVE was assembled for a cost of $210K in 1997, for a price ratio of 10. From Table 2 we see that it becomes cost effective to use the HIVE for this algorithm for image sizes of roughly 432x336 pixels (4 spectral bands) or larger.
Table 3 lists comparative times for the HIVE and the Cray T3E. The wall clock times are only for the portion of the algorithm that runs on the HIVE or on the Cray T3E. It does not include the data reformatting and a large part of the data I/O, and does not include the final stage of the processing that always occurs on the SunULTRA workstation. As Table 3 shows, the HIVE implementation runs typically 1.3 to 1.8 times faster than the Cray T3E implementation. This does not include the time spent waiting in the Cray T3E batch queue (there is no queue on the HIVE). Since the Cray T3E costs about $18M and the HIVE cost only $0.21M, the cost ratio of the Cray T3E versus the HIVE is about 86. Using an approximate average execution time ratio of 1.5, the cost/performance ratio of the Cray T3E versus the HIVE is approximately 130. We should note that this remarkably high cost/performance ratio is not an indication of the general purpose cost/performance ratio of the Cray T3E versus the HIVE.
How can the remarkable performance of the HIVE versus the Cray T3E be explained? One main reason is that this application is particularly well suited for the HIVE since it has minimal interprocessor communication and coordination. Thus, the HIVE is not hampered by its less efficient interconnection network. Also, as noted in section 4.2, for a large problem requiring 512 tasks, the average MIMD parallel utilization on the HIVE is about 40% versus only about 11% on the Cray T3E. Because of this, the Cray T3E, with its 512 processors, only has a 1.1 times advantage in parallelism for this application (11%/40% * 512processors/128processors). Another factor is the Cray T3E is a 64-bit machine while the Pentium Pro is 32-bits. Thus, integers and floats are twice as long on the Cray T3E, forcing the Cray T3E to move around twice the data for the same amount of processing on the Pentium Pro-based HIVE. This is compounded by the fact that the Pentium-Pro has 256 KB secondary cache per processor, while the Cray T3E has only 96 KB. Thus the Cray T3E has to move around twice the data while having available just under two-fifths the amount of cache. Finally, the HSEG algorithm makes heavy use of pointers, which may be less efficient on the Cray T3E.
Acknowledgments
Thanks to Dr. Thomas Clune of Silicon Graphics for technical information on the Cray T3E, and to Dr. Udaya Ranawake of CEDIS and Dr. John Dorband of NASA for technical information on the HIVE.
References:
- R. A. Schowengerdt, Remote Sensing, Models and Methods for Image Processing, 2nd ed., chap. 5, Academic Press: Chestnut Hill, MA, 1997.
- R. M. Haralick, "Statistical and structural approaches to texture," Proceedings of the IEEE, Vol. 67, pp. 786-804, 1979.
- J. C. Tilton, D. Han and M. Manohar, "Compression Experiments with AVHRR Data," Proceedings of the Data Compression Conference (DCC'91), Snowbird, UT, pp. 411-420, April 8-10, 1991.
- K. S. Fu and J. K. Mui, "A survey on image segmentation," Pattern Recognition, vol. 13, pp. 3-16, 1981.
- J. C. Tilton, "Image segmentation by region growing and spectral clustering with a natural convergence criterion," Proc. of the 1998 International Geoscience and Remote Sensing Symposium, Seattle, WA, July 6-10, 1998.
- J. C. Tilton, "Experiences using TAE-Plus command language for am image segmentation program interface," Proc. TAE Ninth Users' Conf., New Carrollton, MD, pp. 297-312, 1991.
- A. Baraldi and F. Parmiggiani, "A neural network for unsupervised categorization of multivalued input patterns: an application to satellite image clustering," IEEE Trans. Geoscience & Remote Sensing, vol. 33, no. 2, pp. 305-316, 1995.
- R. P. H. M. Schoenmakers, Integrated Methodology for Segmentation of Large Optical Satellite Image in Land Applications of Remote Sensing, Agriculture series, Catalogue number: CL-NA-16292-EN-C, Luxembourg: Office for Official Publications of the European Communities, 1995.
- A. Geist, et al, PVM: Parallel Virtual Machine - a users' guide and tutorial for networked parallel computing, The MIT Press: Cambridge, MA, 1994.
- D. J. Becker, T. Sterling, D. Savarese, J. E. Dorband, U. A. Ranawake, C. V. Parker, "Beowulf: A parallel workstation for scientific computation," Proc. Int. Conf. on Parallel Processing, 1995.
Table 1. Listed here are the number of PEs or tasks required, which recursive levels make 4 immediate calls, and which recursive levels make 2 immediate calls and 2 delayed calls for several different levels of recursion. Also included is the image size that could be processed for each of the levels of recursion assuming the image size at the base level is 32 by 32 pixels.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 2. End-to-end wall clock run times for the recursive implementation of the hybrid image segmentation algorithm on the HIVE and on a 167-MHz SunULTRA Model 170E Workstation. The image processed is a 4-band Landsat MSS scene of north central Canada obtained on Aug. 12, 1984. For this test minregions = 512 and convfact = 1.02.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 3. Wall clock run times for all but the top level of the recursive implementation of the hybrid image segmentation algorithm on the HIVE and on the Cray T3E. The image processed is a 4-band Landsat MSS scene of north central Canada obtained on Aug. 12, 1984. For this test minregions = 512 and convfact = 1.02.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
