Sciences and Exploration Directorate - NASA's Goddard Space Flight Center

Numerical Relativity

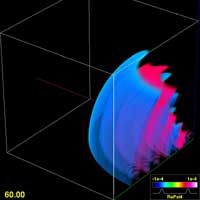
Overview

Numerical relativity is the study of Einstein's equations of general relativity using computer simulations. Groups of scientists around the world, like the group at the Goddard Space Flight Center, are using supercomputer simulations based on Einstein's equations to study how space and time change when very massive objects (like black holes and neutron stars) collide in the universe. The focus of the Goddard group is on applying numerical relativity simulations to model such mergers for gravitational wave and astrophysical applications.

Numerical Simulation Techniques

We have developed a numerical simulation code with adaptive and fixed mesh refinement (AMR/FMR) capabilities based on a general purpose AMR simulation package PARAMESH. Our approach allows us to apply high resolution in the region near the black holes while moving the outer boundary far from the region of interest. We currently use variations of the "BSSN" formulation of Einstein's gravitational field equations, using second and higher-order finite differencing techniques and with hyperbolic-type gauge conditions. We interpret the results of our simulations by applying an array of gauge-invariant analyses including local invariants, horizons, and asymptotic quantities.

Binary black hole gravitational radiation studies

gravitational waveforms from the binary black hole
collision

Click for movie.

A key motivation of our research effort is to provide theoretical support to ongoing and future gravitational wave observations particularly for the LISA project, a joint venture between NASA and the European Space Agency (ESA).

Toward this, part of our effort is focused specifically on questions relating to developing techniques for studying gravitational radiation from binary black hole systems. The studies approach such questions as:

How accurately can we simulate BBH radiation?
How can we characterize "kicks" generated in asymmetric unequal-mass BBH mergers?
What can BBH radiation tell us about strong field interactions in simulations such as spin and spin-orbit interactions?

We are approaching these questions through simulations of approximately head-on binary black hole configurations with varies mass-ratios and spins. These systems provide simple testbeds to study phenomena expected in fully realistic configurations.

Inspiraling binary black holes

A key class of simulations directly relevant to astrophysical BBH configurations involves black holes approaching each other on from a shrinking, approximately circular orbit. As we develop our techniques we are expanding our work with inspiraling simulations designed for both short runs with Lazarus-style waveform estimation, and more costly direct simulations of waveforms. Our simulations are presently focused on accurate radiation from near-ISCO initial configurations though we are pursuing techniques which we expect to be applicable to longer-lasting orbital configurations in the future.

Moving black holes

Generally, accurate simulations on binary black hole systems rely on fundamental techniques which can accurately simulate a single moving black hole. The relevance of these studies is increasing as we pursue increasingly long-lasting BBH simulations. We use simulations of the motion of a single black hole as a test bed arena to study such basic simulation properties as constraint preservation and energy and momentum conservation. Using this test bed we are investigating the performance of advances in gauge condition, higher-order finite differencing, AMR, and modifications of the BSSN formalism.

Click here for a movie showing black-hole tracks from a recent long run (QC9).

Supercomputing 2005: Poster

View the Supercomputing 2005 poster (printable PDF)

Snapshot showing the field representing gravitational wave generated from an inspirallying black hole binary.

We model the astrophysical coalescence of comparable-mass, massive black hole binaries for different mass ratios and spins and calculate the resulting gravitational wave (GW) signatures. A key feature of our work is the use of mesh refinement techniques to handle the wide range of physical scales involved, from the black holes (~1M) to the gravitational waves (~10-100M), and to enable extraction of gravitational waveforms in the wave-zones.

Our methodology involves solving a closely coupled system of partial differential equations with many variables on a very large computational domain. Moreover, we use highly structured component- grids that are distributed across many processors, with a significant amount of communication between processors. Our simulations typically require hundreds of gigabytes and run on several hundred processors for hundreds of hours.

Astrophysical motivation guides our simulations. The waveforms determined by these simulations will be applied to analyzing and interpreting observed GW data from the Laser Interferometer Space Antenna (LISA) mission. Linear momentum loss due to asymmetrical radiation of GW in the unequal mass mergers imparts 'kicks' to the merger remnant. High kick velocities from such mergers have the potential to strongly impact our understanding of how massive black holes have developed over cosmological time scales.